soluciondeecuaciondesegundogrado.blogspot.com

¿QUE ES UNA ECUACION DE SEGUNDO GRADO?

Una ecuación de segundo grado o ecuación cuadrática de una variable es una ecuación que tiene la forma de una suma algebraica de términos cuyo grado máximo es dos, es decir, una ecuación cuadrática puede ser representada por un polinomio de segundo grado o polinomio cuadrático. La expresión canónica general de una ecuación cuadrática de una variable es:

DIRENTES METODOD SE SOLUCION

Ejemplo 1

Resuelve por medio de la raíz cuadrada

Solución:

Ejemplo 2

Resuelve por medio de la raíz cuadrada

Solución:

Ejemplo 3

Resuelve por medio de la raíz cuadrada

Solución:

Factorización

Si los coeficientes a, b y c de la ecuación cuadrática  son tales que la expresión  puede escribirse como el producto de dos factores de primer grado con coeficientes enteros, dicha ecuación cuadrática podrá resolverse rápida y fácilmente. El método de resolución por factorización se basa en la siguiente propiedad de los números reales:

Si a y b son números reales, entonces:

a×b = 0   si y solo si  a = 0 o b = 0  (o ambos valen cero)

Esta propiedad se demuestra con facilidad: si a = 0, hemos concluido. Si a ≠ 0, multiplicamos ambos miembros de ab = 0 por 1/a, para obtener: b = 0.

Ejemplo 1

Resuelve por factorización

Solución:

Ejemplo 2

Resuelve por factorización

Solución:

Ejemplo 3

Resuelve por factorización

Solución: El polinomio no se puede factorizar con coeficientes enteros; por tanto, debe de usarse otro método para encontrar la solución.

Completando el trinomio cuadrado perfecto

El método de compleción del cuadrado se basa en el proceso de transformar la cuadrática general  para que quede así: . Donde A y B son constantes. Esta última ecuación se puede resolver fácilmente por medio de la raíz cuadrada, como se explicó en la sección anterior. Así:

Antes de estudiar cómo se resuelve la primera parte, haremos una pausa breve para analizar un problema relacionado con el nuestro: ¿Qué número se le debe de sumar a  para que el resultado sea el cuadrado de una expresión lineal? Hay una sencilla regla mecánica para encontrar tal número: se basa en los cuadrados de los siguientes binomios:

En ambos casos, observemos que, en el miembro derecho, el tercer término es el cuadrado de la mitad del coeficiente de x, que aparece en el segundo término. Esta observación nos lleva directamente a la regla:

Para completar el cuadrado de una expresión cuadrática de la forma

se suma el cuadrado de la mitad del coeficiente de x, o sea:  o sea

Ejemplo 1

Completa el cuadrado de

Solución: Sumamos el cuadrado de la mitad del coeficiente de x, usamos la forma

, por lo que obtenemos:

Ejemplo 2

Completa el cuadrado de

Solución: Sumamos ; o sea , así:

La resolución de ecuaciones cuadráticas por el método de compleción del cuadrado se ilustra mejor con ejemplos

Ejemplo 3

Resuelve  por el método de compleción del cuadrado

Solución:

           Sumamos 2 a ambos miembros de la ecuación para eliminar -2 del miembro izquierdo.

                 Para completar el cuadrado del miembro izquierdo, sumamos el cuadrado del coeficiente de x, en ambos miembros de la ecuación.

     Factorizamos el miembro izquierdo.

                          Resolvemos por medio de la raíz cuadrada.

         

Ejemplo 4

Resuelve  por el método de compleción del cuadrado

Solución:

         Observa que el coeficiente de x² no es 1. En tal caso, dividimos todos los términos entre el coeficiente principal y proseguimos como en el ejemplo anterior.

Formula cuadrática

Para obtener la formula para resolver ecuaciones de segundo grado, tomamos la ecuación general  y resolvemos para x, en función de los coeficientes a, b y c, por el método de compleción del cuadrado; de esta manera obtenemos una fórmula que podremos memorizar y utilizar siempre que se conozca el valor de a, b y c.

Para empezar haremos igual a 1 el coeficiente principal. Para ello, multiplicamos por 1/a ambos miembros de la ecuación. Queda así:

Sumamos –c/a a ambos miembros de la ecuación para suprimir c/a del miembro izquierdo.

Ahora completamos el cuadro del miembro izquierdo; para ello, sumamos a cada miembro del cuadrado de la mitad del coeficiente de x;

Luego factorizamos el miembro izquierdo de la ecuación y la resolvemos por medio de la raíz cuadrada.

Obtenemos esto:

Está última ecuación se llama fórmula cuadrática. Es necesario memorizarla y emplearla para resolver ecuaciones cuadráticas, cuando no dan resultado métodos más sencillos. Observa que b²-4ac recibe el nombre de discriminante y nos proporciona la siguiente información útil respecto de las raíces:

b² - 4ac

ax² + bx + c = 0

Positivo

Dos soluciones reales

Cero

Una solución real

Negativo

Dos soluciones complejas

Ejemplo 1

Resuelve  por la fórmula cuadrática

Solución: anotamos la fórmula cuadrática e identificamos a=2, b=-4 y c=-3.

 Sustituimos la fórmula y simplificamos.

Ejemplo 2

Resuelve  por la fórmula cuadrática

Solución:  escribimos en la forma general e identificamos a = 1, b = -6 y c = 11

 Sustituimos la fórmula y simplificamos.

 ¿COMO SE RESUELVE POR EL METODO DE FORMULA GENERAL?

Consideremos la ecuación general de segundo grado (ecuación cuadrática) que tiene la forma: .
Resolver esta ecuación implica encontrar el valor o los valores de que cumplen con la expresión, si es que existen.
El último método que se estudia para resolver ecuaciones de segundo grado es la "Fórmula General".

Analizando la raíz cuadrada, se llega a las siguientes conclusiones:

Si 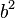es menor que los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un número complejo.

Si 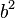es mayor que obtendremos dos valores distintos de X reales.

Y si 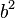es igual que obtendremos dos valores de X reales e iguales.

Al término se le llama discriminante.

tomando en cuenta el orden de los terminos: "a","b"y"c"=x²-6x+9
 

¿COMO SE RESUELVE CON LA FORMULA EXCEL?

Crea un archivo de hoja de calculo Microsoft Excel en “Tu carpeta” llamado Ecuaciones de 2º grado.

       Comenzamos el ejercicio escribiendo todo el texto que nos aparecerá en esta nueva hoja de cálculo:

1.        En la celda C1 escribe: Resolución de ecuaciones de 2º grado. La alineación en esta celda es centrada.

2.        En la celda B3 se escribe: ax² + bx + c = 0.

Nota: Para escribir el exponente de la x utilizamos el código ASCII que se utiliza para escribir caracteres que no están en el teclado. Para escribir el cuadrado de la x mientras se mantiene presionada la tecla Alt en el teclado numérico (a la derecha) pulsamos las teclas que contienen los números 253.

3.        En la celda B5 escribe: Introducción de valores.

4.        En la celda B7 escribe:       En la celda C7 introduce el valor de a

5.        En la celda B8:                   En la celda C8 introduce el valor de b

6.        En la celda B9:                   En la celda C9 introduce el valor de c

7.        En la celda B11:     Discriminante

8.        En la celda B12:     Raíz discriminante

9.        En la celda B14:     Soluciones:

10.    En la celda B15:     1ª solución:

11.    En la celda B16:     2ª solución:

12.    En la celda C3 escribe:       Las soluciones de la ecuación vienen dadas por la fórmula:

13.    Selecciona las columnas B y C; y en el menú Formato elige Columna 4 Autoajustar a la selección.

     Ahora que ya has escrito el texto correspondiente a esta hoja de cálculo, indicamos a continuación como has de introducir las fórmulas necesarias para completar esta práctica.

En la celda D11 se ha de introducir la fórmula que calcule el discriminante.

Como la pretensión es que esta hoja de cálculo sirva para resolver cualquier ecuación de 2º grado con soluciones reales, hemos de operar con contenidos de celdas, por ello en lugar de valores en las fórmulas aparecerán referencias a celdas.

Nota: No te preocupes si el resultado de la fórmula son mensajes de error, pues todavía no hemos introducido datos. No obstante, si el discriminante es negativo, la raíz del discriminante siempre será un valor de error, pues como sabes las raíces de números negativos no son valores reales.

1.          Para que calcule el discriminante escribiremos en la celda D11 lo siguiente:   =C8^2-4*C7*C9

2.        Observa que dato de la ecuación corresponde a cada una de las referencias del celda que aparecen en la fórmula anterior.

3.        En la celda D12 escribe la expresión (o inserta la función) que calcule la raíz del discriminante, esto es =Raiz(D11)

En la celda C15 se escribe la expresión que da lugar a una de las soluciones de la ecuación de 2º grado. Recuerda que la raíz del discriminante se ha calculado en la celda D11, por tanto

4.        En la celda C15   escribe:  

=(-C8+D12)/(2*C7)

5.        En la celda C16 escribimos la expresión que da lugar a la segunda solución de la ecuación:

=(-C8-D12)/(2*C7)

6.        Observa que dato corresponde a cada una de las referencias del celda que aparecen en la fórmula anterior

       Vamos a utilizar una de las funciones lógicas que posee Excel para que la hoja de cálculo nos informe según el signo del discriminante, si la ecuación posee o no soluciones:

La función que vamos a utilizar es la función SI que ya conoces, de la unidad 8. Para saber más sobre esta función recuerda que puedes consultar la Ayuda de Microsoft Excel.

1.        En la celda E11 escribe todo seguido, respetando los paréntesis, los puntos y comas, y las comillas lo que a continuación indicamos:

=SI(D11<0;"El discriminante es negativo";SI(D11=0;"El discriminante es cero";"El discriminante es positivo"))

2.        En la celda D15 escribe:

=Si(D11<0;"La ecuación no tiene soluciones reales";Si(D11=0;"La ecuación posee una solución doble";"La ecuación posee dos soluciones reales y distintas"))

       Todavía podemos mejorar nuestra práctica insertando como objetos de dibujo las fórmulas, tal y como estamos acostumbrados a escribirlas. Es decir, el discriminante:, la raíz del discriminante y la expresión que determina las soluciones de la ecuación:  

Para ello hemos de utilizar la herramienta de Office llamada Editor de ecuaciones. A continuación iremos detallando los pasos.

1.        Sitúate en la celda C11, y haz clic en el menú Insertar, Objeto.

2.        En el cuadro de la ventana localiza Microsoft Editor de ecuaciones y haz clic en el botón Aceptar. En el caso de que no lo tengas continúa en el siguiente apartardo. No obstante, si realizas la práctica 5 llamada Microsoft Editor de ecuaciones, aprenderás a instalarlo.

La figura 2 muestra la barra de herramientas del editor de ecuaciones

Ten en cuenta

que para desplazarte por la expresión que estás escribiendo con el editor de ecuaciones se utilizan las teclas del cursor. Como ejemplo, observa la figura 3.

 

3.        Trata de escribir la expresión  en la celda C11

4.        Haz lo mismo con las otras dos expresiones en la celda C12 y  en la celda E5.

       Puedes mejorar la presentación de la práctica cambiando las fuentes, los anchos de columna, bordes, sombreados de celda, etc.

       Nos disponemos a resolver ecuaciones de 2º grado. En las celdas C7, C8 y C9 se introducirán los números correspondientes a los coeficientes  a, b y c.

1.        Introduce los datos correspondientes a la ecuación 5x²-2x-1=0 y observa los resultados.

2.        Del mismo modo, introduce los datos de cada una de las siguientes ecuaciones:

x²-2x+1=0;   2x²+3x+4=0;  x²+4x+3=0

GRACIAS POR SU TIEMPO DE LEER ESTO....